| |
|
Pendulum Oscillation(钟摆震荡)
The differential equation to describe oscillation of a pendulum of length l is
This is a nonlinear equation. For small oscillation amplitude,
it can be linearized as
The oscillation frequency is thus given by
As the amplitude increases, the oscillation frequency becomes smaller. The frequency corrected for a finite amplitude is approximately given by
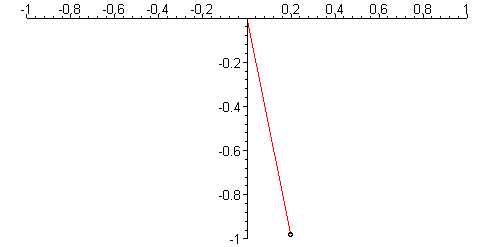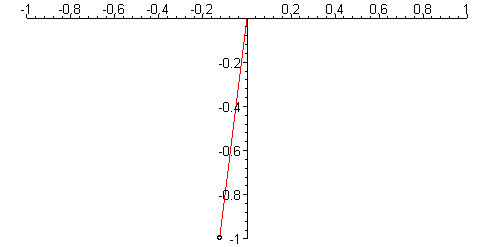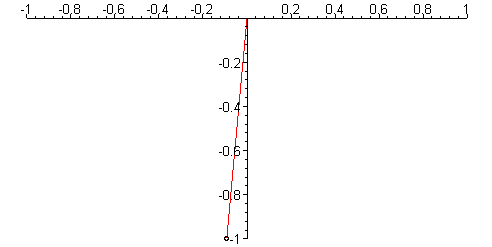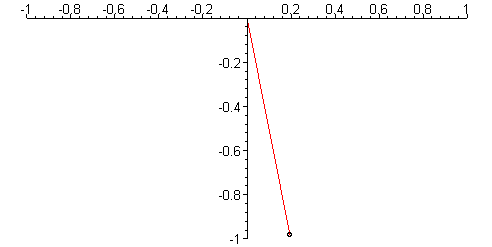
Animation shows oscillations with small and large amplitude,
with(plots):
k1:=1/sqrt(2.):
k2:=0.1:
a:=[seq(plot([[sin(2*arcsin(k1*JacobiSN(1.8+0.25*(i-1),k1))),-cos(2*arcsin(k1*JacobiSN(0.25*(i-1)+1.8,k1)))]],style=point,symbol=CIRCLE,color=black),i=1..30)]:
b:=[seq(line([0,0],[sin(2*arcsin(k1*JacobiSN(1.8+0.25*(i-1),k1))),-cos(2*arcsin(k1*JacobiSN(0.25*(i-1)+1.8,k1)))],color=red),i=1..30)]:
aa:=display(a,insequence=true,axes=normal,view=[-1..1,-1..0]):
bb:=display(b,insequence=true,axes=normal,view=[-1..1,-1..0]):
display({aa,bb});

Amplitude = 0.1
with(plots):
k1:=1/sqrt(2.):
k2:=0.1:
c:=[seq(plot([[sin(2*arcsin(k2*JacobiSN(0.25*(i-1)+Pi/2,k2))),cos(2*arcsin(k2*JacobiSN(Pi/2+0.25*(i-1),k2)))]],style=point,symbol=CIRCLE,color=black),i=1..27)]:
d:=[seq(line([0,0],[sin(2*arcsin(k2*JacobiSN(0.25*(i-1)+Pi/2,k2))),-cos(2*arcsin(k2*JacobiSN(Pi/2+0.25*(i-1),k2)))],color=red),i=1..27)]:
cc:=display(c,insequence=true,axes=normal,view=[-1..1,-1..0]):
dd:=display(d,insequence=true,axes=normal,view=[-1..1,-1..0]):
display({cc,dd});
-------------------------------------------------------------------------------- |
|